[Post 1] Goalie Consistency: Does it matter?

Goaltenders make up the least predictable position in hockey. Their behavior confounds analysts and casual fans alike. It isn’t uncommon for a strong goalie to have a below replacement level year, or for an unknown goalie to come in and dominate the league. This may partly explain the relative dearth of analysis on goalies - they're voodoo, it's often said.

That's where this series of posts comes in. Ideally, it will help - even marginally - rectify this dearth. I’m going to explore the idea of consistency in goalies, along with its potential attendant effects on standing points, current performance, and future performance.

But before that, in this post, I'll briefly explain a few concepts that will come up across the series.

Poisson Distribution

Goals have been shown to follow a Poisson process. Fortunately, the Poisson is easy to simulate. Here’s what 100,000 simulations of goals allowed in a game look like when a goalie is expected to allow 3 goals.

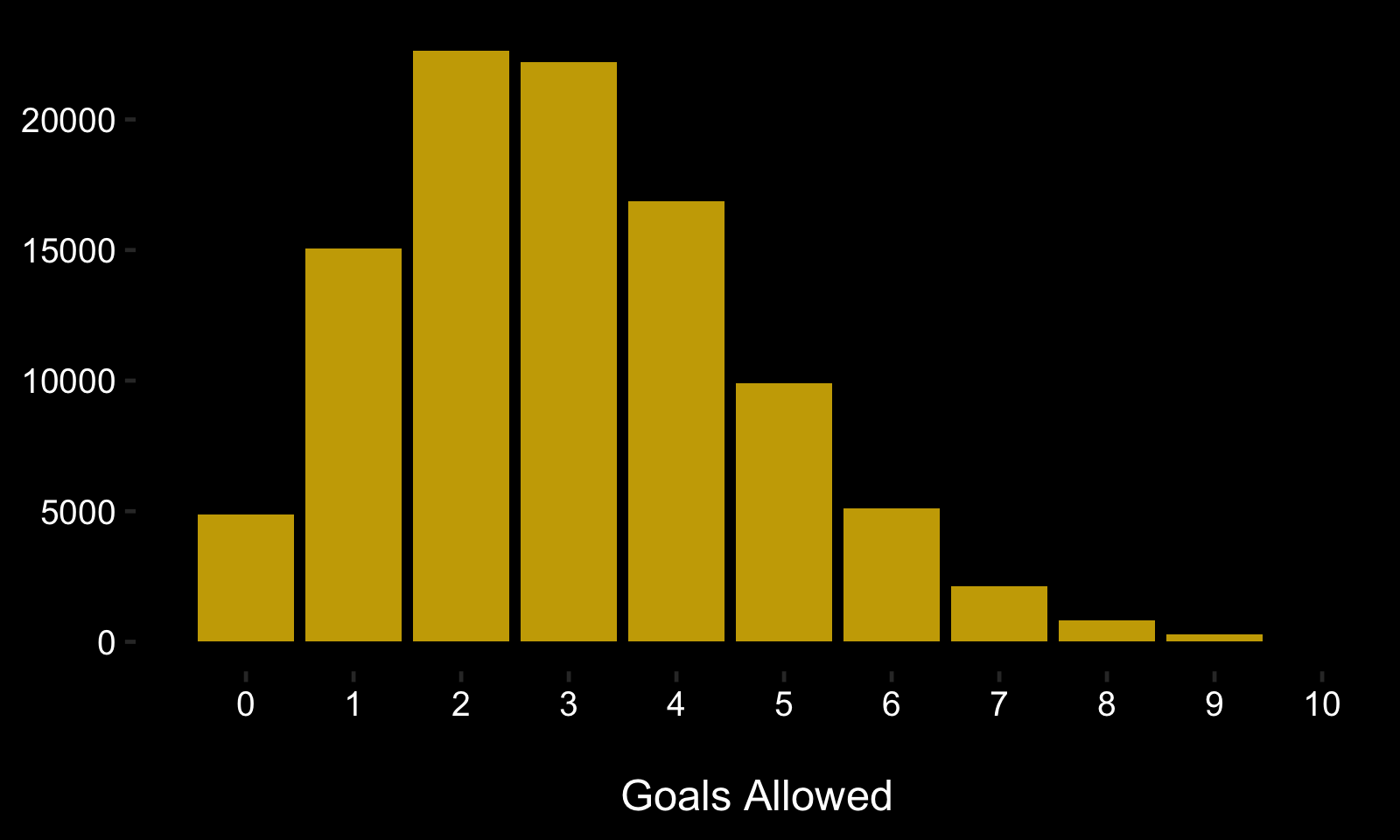
The simulation of the Poisson to obtain outcomes for an exploration on inter-game goalie consistency occurs in the second post of this series.

Entropy

Entropy is a popular concept in information theory. It measures the orderliness in a sequence, usually of binary events. Good news - shots can be expressed as a sequence of binary events. Here’s what a sequence of outcomes from shots on goal can look like (1 goal, 0 save).

Because of this, entropy can be used to measure the inter-shot consistency of goalies.

The application of entropy as a measure of consistency in sport was first (I think!) introduced here, and then repurposed for teams and shooters in hockey. We adapt this previous work to obtain the starting formula for goalie entropy (below).

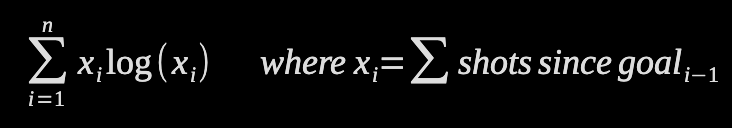
Since entropy sums streaks of saves, it follows that higher entropy equates to a lack of consistency - or conversely that low entropy equates to consistency.

Entropy is used to explore inter-shot goalie consistency in the second post of this series.

There's a problem though. This starting formula doesn't account for the length of a goalie season, nor does it account for the percentage of shots saved - both of which have an effect on entropy. It needs to be adjusted if we're going to compare it between goalies and between seasons.

Normalized Entropy

To address this, the xi’s in the entropy formula above are divided by the number of shots a goalie faces in a season, and then the entropy itself is divided by the number of goals a goalie allows in a season (plus one). After this, the entropy for each goalie is compared to that of 10,000 randomly generated (by sampling without replacement) seasons having the same performance - it becomes a percentile.

Up to now, this follows exactly the previous work on shooters.

There is still a problem, though - all shots are currently considered equal. But it has been proven many times that we should expect different goal rates for different shots. Thankfully, Peter Tanner makes his work on Expected Goals available for public consumption. His take on them is summarized below.

Expected Goals

Tanner, through his website MoneyPuck, provides detailed data for each unblocked shot that occurs in the NHL (whether it hit the net or not) along with a prediction - the probability of the shot being a goal. His model includes information such as “the distance from the net, angle of the shot, type of shot, and what happened before the shot” among other things.

The expansion of normalized entropy to include expected goals is outlined in the third post of this series.

Posts in this series: [Post 1] The effect of inter-game goalie consistency on expected standing points [Post 2] The effect of inter-shot goalie consistency on expected standing points [Post 3] The effects of inter-shot goalie consistency (using real data)