An Application of Prospect Pick Probabilities [Part 2]
In An Application of Prospect Pick Probabilities, I introduced a new perspective on draft pick value using Prashanth Iyer and I's draft probability tool. Here, I extend the methodology to include prospect value uncertainty.
Accounting for Uncertainty
One of the main considerations for teams drafting in the 2-7 spot this year was whether they should risk their extremely valuable lottery pick on Matvei Michkov. He signed a 3-year contract in Russia. He only met with a few teams. He might be the most talented player in the draft. He may never come to North America... etc. Essentially, the question these teams were asking is this: is it worth drafting Michkov's uncertainty when more reliable, though perhaps less skilled, players are available? Once again, teams have to make a complex calculation. Once again, they're left with mostly instinct.Unless!
Unless, prospect value uncertainty is quantified and included in the decision process.
Assigning Uncertainty
Adapting the previous post to include uncertainty is actually easy. Instead of assigning prospect values through point estimates (Bedard was at 24 WAR, Michkov at 17.5), prospects are assigned probability distributions which reflect the uncertainty of their value.As an example: instead of Bedard's value being 24 WAR, it will be normally distributed with mean 24 and standard deviation 3. Here's what that looks like:
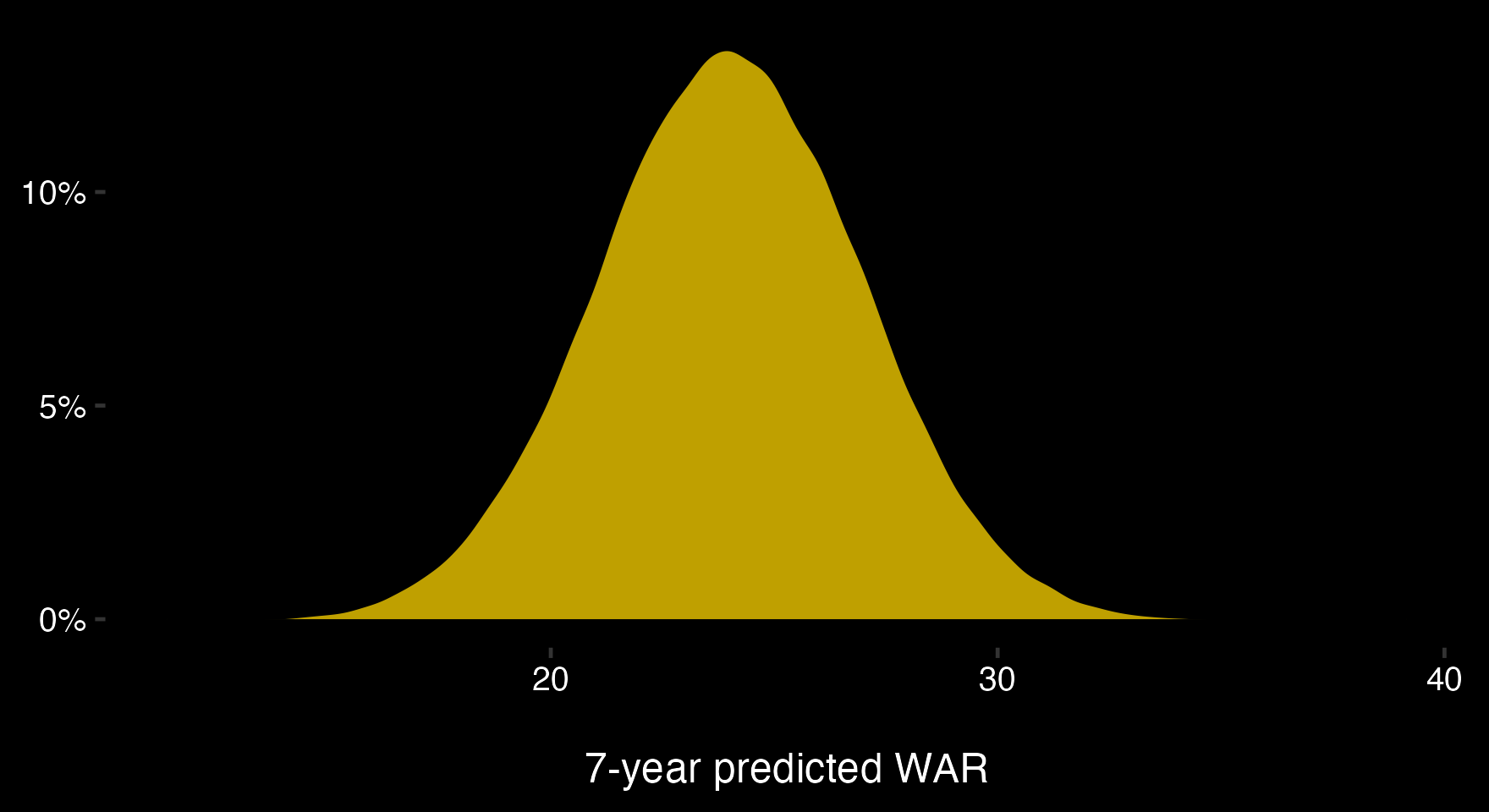
In this example: - Bedard has a 50% chance of providing 22-26 WAR. - Bedard has a 25% chance of providing 26+ WAR. - Bedard has a 25% chance of providing -22 WAR.
Like the point estimates in the first post, the actual distribution doesn't matter, it's just an example to illustrate the framework I'm introducing.
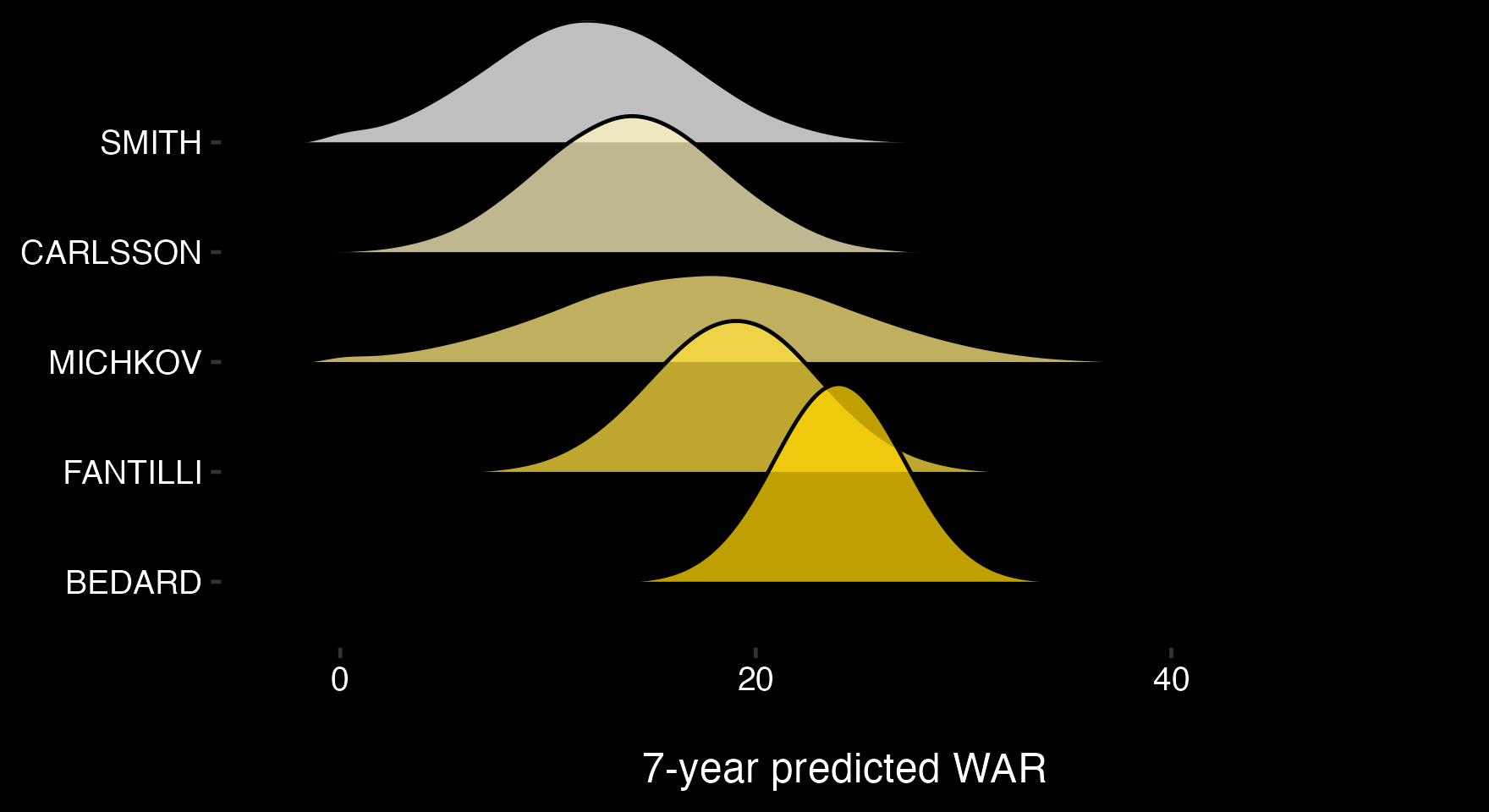
Let's assign these value distributions to each player, making sure Michkov's value has higher uncertainty by increasing the standard deviation of his distribution. Prospect values now look like this:
Then, these probability distributions are multiplied by the probability a prospect is available at each pick, as in the previous post. Pick values now look like this:
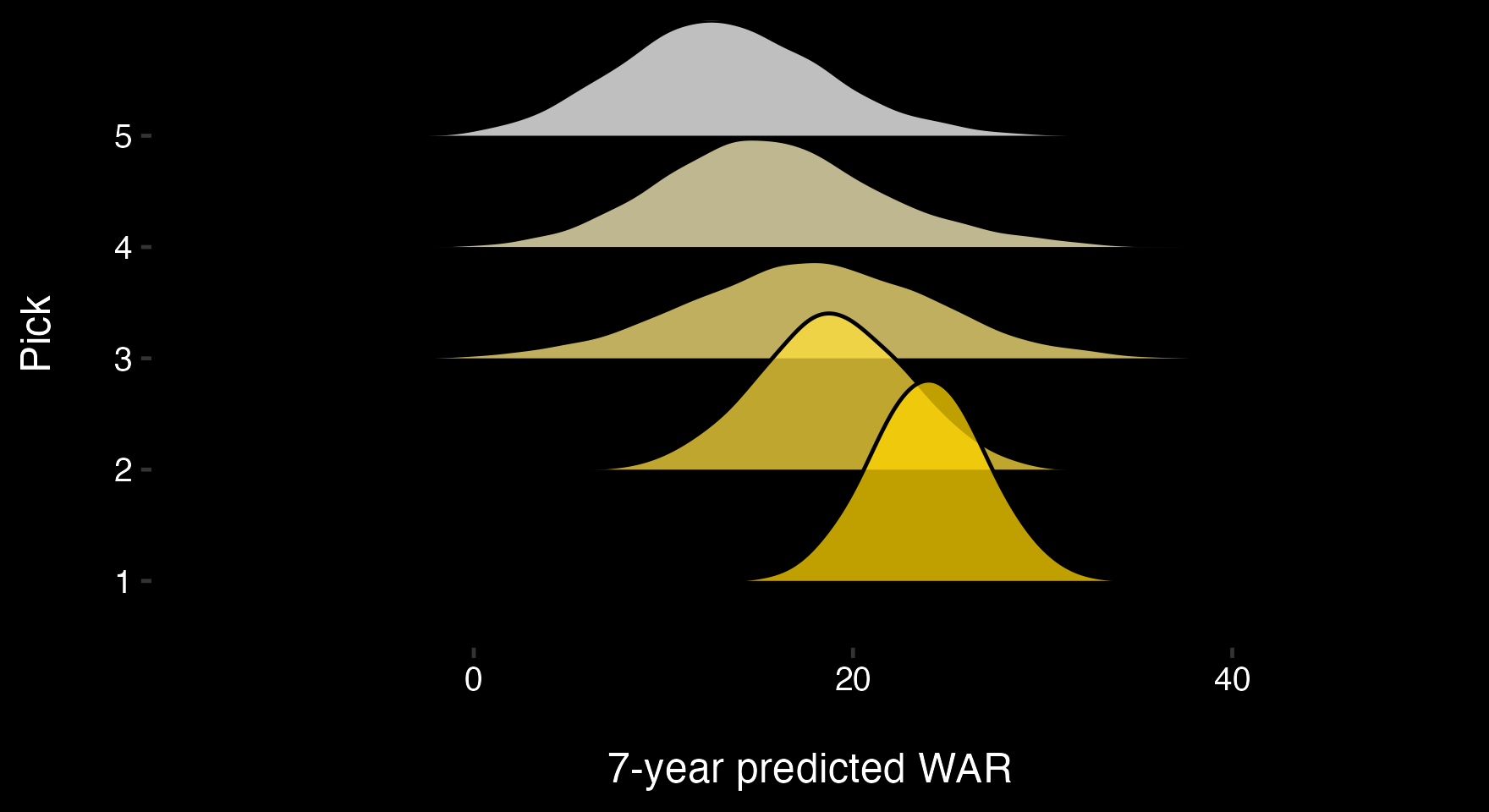
With these pick value distributions you get the same comparisons as you did in the previous post, plus: - the probability that a given pick will be more valuable than another. - WAR for whichever "outcome" you're interested in (like top 10% scenario, bottom 10%, etc.)
Let's re-visit the Montreal example where I suggested they should only trade up if the value of the fourth pick (15.87) exceeded that of their package (fifth pick (13.15) plus a piece). After including uncertainty, these point estimates become probability distributions and the difference between the two picks looks like this:
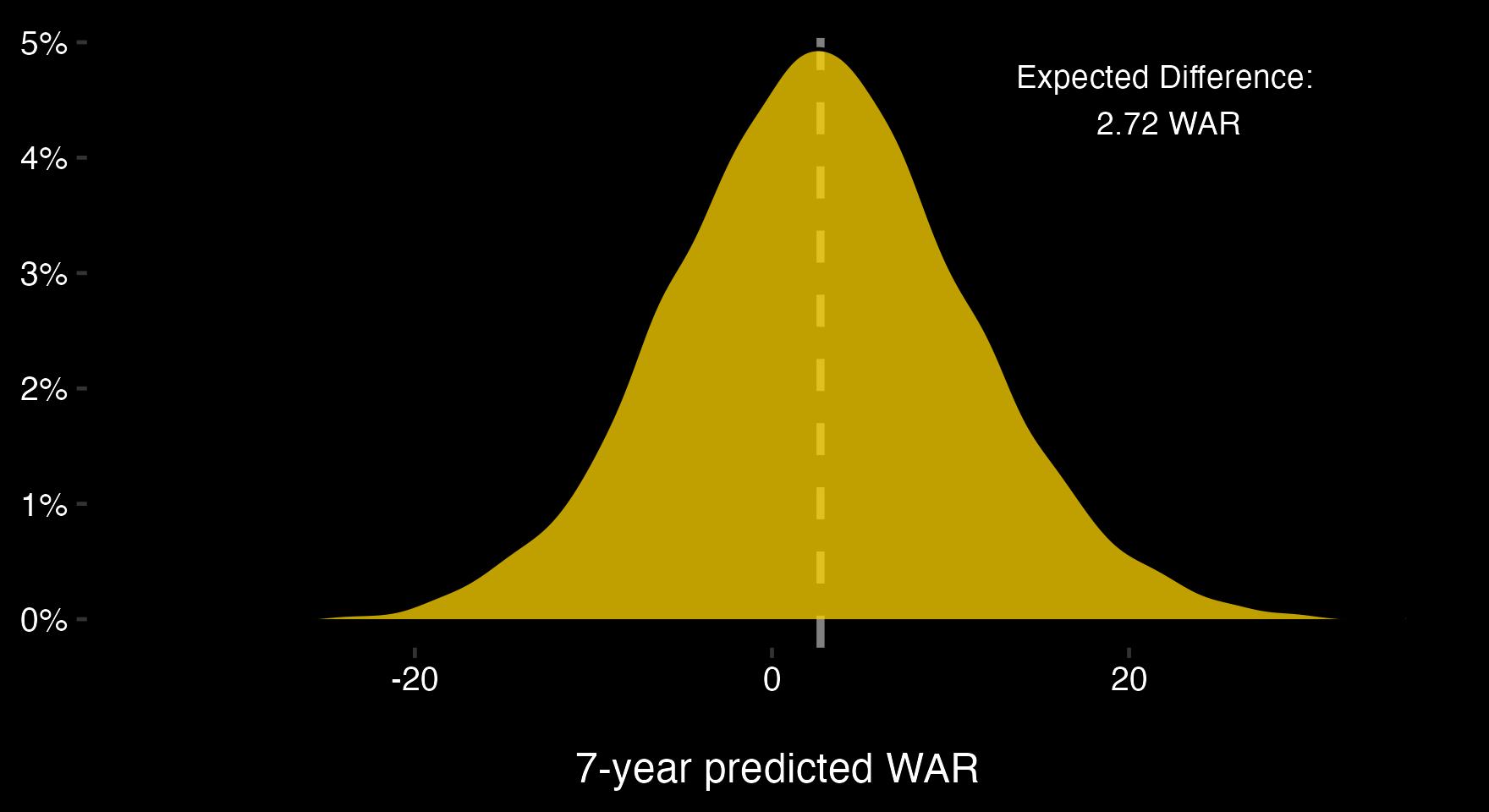
Code available here: https://github.com/spazznolo/draft-rankings/blob/main/scripts/post_4.R