[Post 3] Is the overtime random after each shot?

To measure this, we'll regress various team and game characteristics, including who had the last shot, on the outcome of individual games which ended in overtime. Specifically, the predictors will be: a team's xGF% throughout their season, game and overtime (before the winning goal was scored), and whether they had the last shot before the winning goal was scored. Think of the non-shot predictors as controls. A few examples of what an observation looks like:

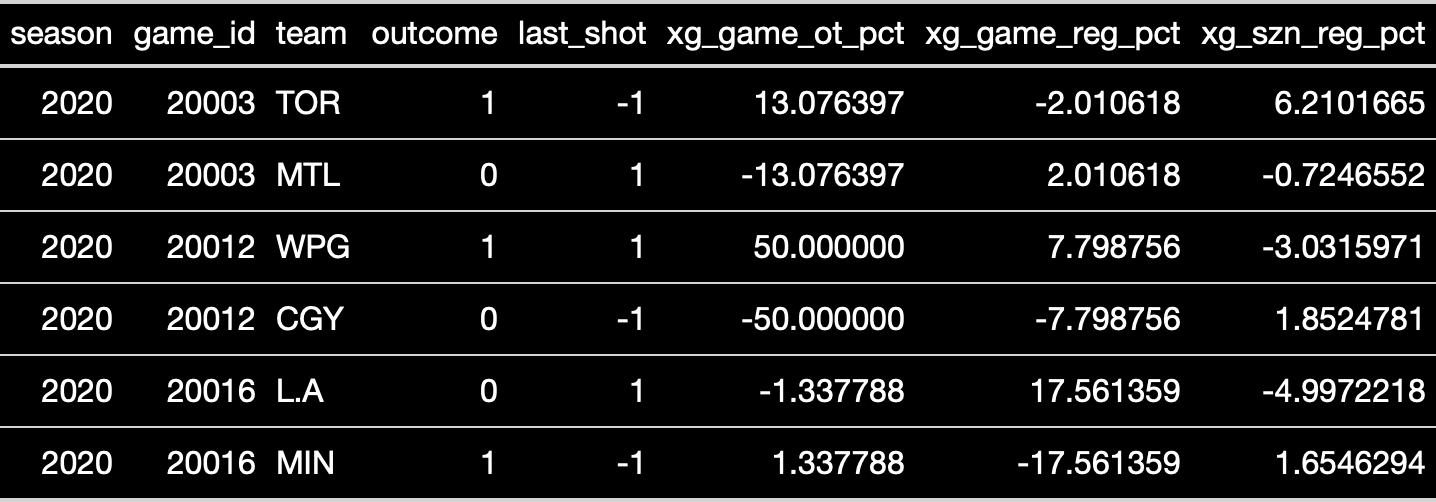
Using every game that ended in overtime since its inception in 2015, the regression can be summarized like this:

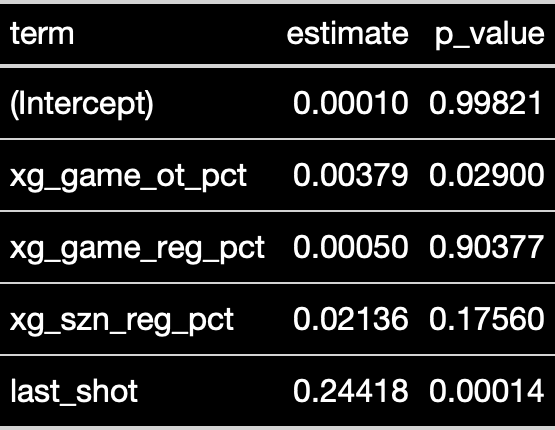
Model Translation:

Having the last shot matters - it adds about 13.8% to a team’s win probability (63.8%).

The only other relevant predictor is a team's xGF% in the overtime before the goal was scored. It's a distant second though: a 10% increase in xGF% adds about 1.9% to the team's win probability. This means that if a team dominates overtime with 75% of Expected Goals, its probability of winning only increases 4.7% (54.7%).

A team's xGF% in the regular season and in a given game's regulation did not factor.

Are all shots equal, though?

In this model, all shots were considered equal. Given that the last shot before the goal is the most important factor in the outcome of an overtime, we shouldn't just treat them equally, however. Some questions: Do all shots lead to a higher chance in winning? Can we include games that did not end in the overtime to make the analysis more robust? Doesn't every shot matter, and not just the last ones?

In the next post, we'll build a win probability model based on each given shot's characteristics.